Similarity conditions

The similarity theory requires that three essential conditions be met for hydraulic model tests: geometric (length), kinematic (velocity) and dynamic (forces) similarity between the model (M) and the full-scale version (G). Kinematic and dynamic similarity are grouped together under the heading of physical similarity (see Affinity laws).

Geometric similarity

In order to fulfil the condition of geometric similarity, all the linear dimensions of the model pumps (I_M) and the corresponding dimensions of the full-scale version ("prototype") (I_G) must have the same ratio (m_I; model scale):

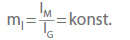
The geometrically similar reproduction of a pump and its system environment in model form is only required for sections relevant for the actual flow analysis. Establishing geometric similarity on the discharge side of the system is irrelevant if the fluid flow analysis is confined to the pump's suction side.

The full-scale version's wall surface roughness can only be reproduced in the model with limited accuracy, which is insufficient to achieve a microscopic level of geometric similarity, meaning that the boundary layer flow and the resultant  pressure losses arising due to wall friction can only be examined to a limited extent.

Kinematic similarity

Kinematic similarity requires the proportionality of the corresponding velocity vectors in the model (v_M) and the full-scale version (v_G) (see Velocity triangle). The requirement of a constant velocity scale can strictly speaking only be fulfilled in conjunction with geometric and dynamic similarity:

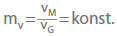
Any deviation from geometric similarity will result in a roughly equal deviation from kinematic similarity. In model tests, deviations from kinematic similarity often manifest themselves via discrepancies between the degree of turbulence in the model flow and the flow in the full-scale version. This degree of turbulence has an influence on the change from laminar to turbulent flow (see Boundary layer, Fluid mechanics), on the possible occurrence of flow separation, and therefore on flow losses. Often, these cannot be assessed with sufficient accuracy on a model.

Experience has shown that the different types and structures of the boundary layers in the model and the full-scale version result in only minor deviations from kinematic similarity provided that there are no significant differences in flow separation zones and investigations are not concerned with areas close to surfaces such as those of vanes.

Dynamic similarity

In order to fulfil the requirement of dynamic similarity, a defined scale ratio (m_f) must apply to all forces (F) which determine flow phenomena in both the model (M) and the full-scale version (G).

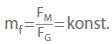
Apart from the two-phase effects in two-phase flow, the forces of significance in hydraulic pump modelling are inertia, gravity, pressure and friction.

Dynamic similarity with regard to the inertia and gravity forces in a model and full-scale version is expressed by the fact that the Froude number (Fr) is constant:

v   Characteristic flow velocity
l    Characteristic length
g   Local acceleration due to gravity

The same applies to the Reynolds number (Re):

Re_M = Re_G

v    Kinematic viscosity of the fluid handled

Dynamic similarity with regard to the pressure and inertia forces present in the model and the full-scale version is expressed by the same values of the  Euler number (Eu):

Eu_M = Eu_G

P    Characteristic pressure (pressure difference)
ρ    Fluid density
g    Local acceleration due to gravity

In the case of centrifugal pumps, the Euler number expresses the relationship between the pressure rise in the pump (i.e. the characteristic pressure difference) and the circumferential velocity at the impeller outer diameter (u₂) (i.e. the characteristic velocity) and is as such termed the head coefficient. Achieving the same Euler number or head coefficients in both the model and the full-scale version requires that both geometric and kinematic similarity are ensured and that the same Froude and Reynolds numbers are present in both the model and the full-scale version.

When transient flows with a frequency f are involved, the Strouhal number comes into play. In hydraulic modelling, a frequent deviation from dynamic similarity arises from the fact that the Froude or Reynolds numbers in the model and in the full-scale version are not the same due to technical reasons relating to the tests. Many years of experience have enabled certain ranges of these numbers to be obtained in the model and the full-scale version without substantially impairing physical similarity (see Efficiency scale-up).